Today we look at our completed display of rectangle charts and create a newsletter for our families telling them about our findings.
Adaptation for ESOL students: Check that all students understand the key words for this section -a decade, a census, a product.
Display the factor charts, in order, for the class to examine.
Encourage the children to look at the charts and write statements (in pairs) about their observations. The following questions may be used as prompts for the children.
Share statements. Use these statements to form the basis for the newsletter home. In addition to the class statements you may like to include the following brainteaser.
A census taker approaches a house and asks the woman who answers the door.
"How many children do you have, and what are their ages?"
Woman: I have three children. The product of their ages is 36, the sum of their ages is equal to the address of the house next door."
The census taker walks next door, comes back and says to the woman.
"I need more information."
Woman: "I have to go. My oldest child is sleeping upstairs."
Census taker: "Thank you, I have everything I need."
Question: What are the ages of the each of the three children?
This week we send home a class newsletter, which shares our findings of the week. In the newsletter is a brainteaser for the family to work on.
For a start we have to find all of the sets of three numbers whose product is 36. These can be found systematically. We do this below but we also find the sum of the factors as this is part of the problem.
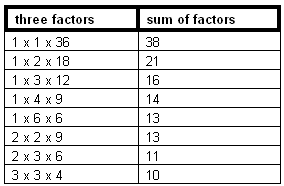
From the table the census taker would have known the ages of the children if the number of next door was anything but 13. But he still needed some more information so the number had to be 13.
When the woman said that she had an eldest child then the ages had to be 2, 2 and 9 (rather than 1, 6 and 6). So that's how the census taker worked out the ages of the children.
Published on: 09 Jan 2018
